Normal Mode Summation for calculating the synthetic seismogram for a string

When we pluck a string fixed at both ends, then this will creating a standing wave. We can get some insights on the behavior of the propagating wave by considering normal modes or free oscillations of the string.

A wave propagating along the string follows the 1D scalar wave equation.

Since, the string has fixed ends, it satisfies the boundary conditions (zero displacement at the fixed ends) and this lead to the vibration of the string at only specific frequencies called eigenfrequencies. The eigenfrequencies are separated by pi*v/L, where v is the velocity of the wave and L is the length of the string. The velocity of the wave depends on the material of the string. Since, the eigenfrequencies are inversely proportional to the length of the string, the longer the string, closer the eigenfrequencies become.

Each eigenfrequencies correspond to a solution of space_term*time_term where the spatial term is known as the spatial eigenfunction.

A traveling wave is the weighted sum of the string’s normal modes. Hence, it is the sum of the eigenfunctions times its amplitude (function of the eigenfrequency). Thus, the real propagating wave is the interference of different modes of the string.

The amplitude for each eigenfunction depends on the position of the source that generated the waves and on the behaviour of the source as a function of time.

We can consider a very simple function to model the behavior of the source as a function of time

F(wn)=exp[-(wn*tau)^2/4]    (Stein and Wysession)

The shape of the source depends on the value of tau.

Let us make a program to calculate a synthetic seismogram using the normal mode summation (see Stein and Wysession (2003) pg. 466). We first keep the parameters same as the Stein and Wysession.

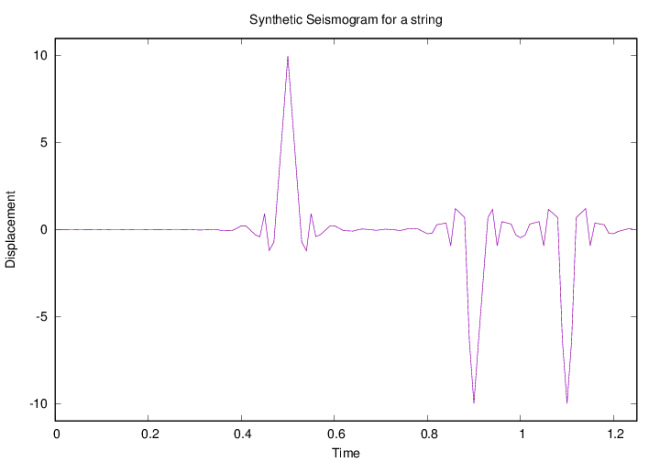
We consider a string of length 1m with a wavespeed 1m/s, a source at 0.2 m and the receiver at 0.7 m. Here, we add 200 modes to get the synthetic seismogram. The seismogram length is 1.25 sec and the time steps is 100.

program synt_seis_strings
    implicit none
    real, parameter :: pi = 4*atan(1.0)
    real :: stln,vel,xsrc,xrcvr,tseis,dt,tau,npiL,srctm,rcvrtm,wn,Fwn,spctm,coswt
    integer :: i,n,j
    integer, parameter :: nmode=200    !number of modes (nmode)
    integer, parameter :: nt=100    !number of time steps(nt)
    real(kind=16), dimension(1:nmode) :: Uxt
    real(kind=16), dimension(1:nt) :: Umode
    character*12 :: filename

    
    print *, 'Enter the string length (ex: 1.0):'
    read *, stln

    print *, 'Enter the wave speed: (ex: 1.0):'
    read *, vel
    

    print *, 'Enter the position of the source (in m) (ex: 0.2) :'
    read *, xsrc
    
    print *, 'Enter the position of the receiver (in m) (ex: 0.7) :'
    read *, xrcvr

    print *, 'Enter the duration of the seismogram (in sec) (ex: 1.25) :'
    read *, tseis

    dt=tseis/nt    !time step in sec
    tau=0.02    !source shape term

    
    do 5 i=1,nt
        Uxt(i)=0.0
    5 continue
    do 10 n=1,nmode
        npiL=n*pi/stln
        srctm=sin(npiL*xsrc)    !source term
        rcvrtm=sin(npiL*xrcvr)    !Receiver term
        wn=n*pi*vel/stln    !mode frequency
        Fwn=exp(-((tau*wn)**2)/4)    !weighting factor of different frequencies

        spctm=srctm*rcvrtm*Fwn        !space term
        
        do 15 j=1,nt
            coswt=cos(wn*dt*(j-1))    !time term
            Uxt(j)=Uxt(j) + coswt*spctm    !displacement
        15 continue
    
    10 continue
        open(unit=1,file='seism.dat')
        write(1,'(f6.2,f12.6)') (dt*(j-1),Uxt(j), j=1,nt)    !writing the displacement
        close(1)
        
        
    stop
end program synt_seis_strings

The synthetic seismogram data is saved in the file seism.dat. Now, we run the above program and plot the output.

#!/bin/bash

prog="synt_seis_strings.f" #fortran program name
exect=`echo $prog | cut -d"." -f1` #executable name

rm -f *.dat $exect #remove files

gfortran -ffree-form $prog -o $exect #compiling the fortran program
./$exect #running the executable

datascrpt='modesPlot.gp'
echo "plot [0:1.25][-8:8] 'seism.dat' using 1:2 w lines " >$datascrpt

#######GNUPLOT##################
gnuplot << EOF
fignm='synth_seis.ps'
figtitle='Synthetic Seismogram for a string'
datafile=system("echo $datascrpt")

xlb="Time"
ylb="Displacement"
set terminal postscript color solid #terminal type
set title figtitle #figure title
set xlabel xlb #xlabel
set ylabel ylb #ylabel
set output fignm #output fig name
unset key
load datafile
EOF

In the above figure, we can see three peaks. First peak at 0.5s is the direct arrival from the source to the receiver. The distance between the source and receiver is 0.5. So the time taken from the source to the receiver is 0.5/1=0.5 sec.

The other two inverted peaks are the reflected arrivals. It is the time taken by the wave from the source to reach the end and reflected back to reach the receiver. The first reflected phase we observe is at 0.9s. It it due to the reflection from the left boundary. This can be calculated ((0.2-0)+0.7)/1=0.9 sec. Similarly, the other arrival (reflected phase from the right boundary) could also be calculated.

We have used the exponential source term (F(wn)=exp[-(wn*tau)^2/4] ) which depends on the value of eigenfrequencies and tau. We have modeled its dependency.

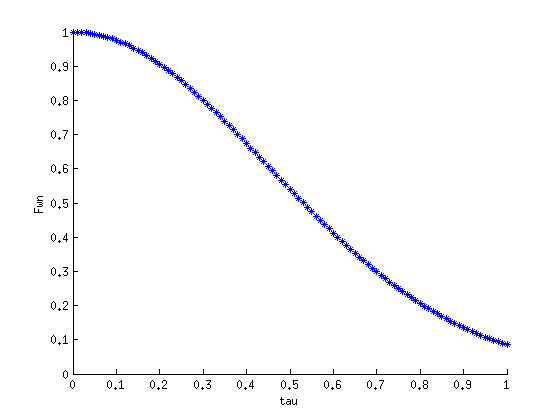
In the second figure, we have considered the value of wn=3.14.

Here, also we have considered the source term to be an exponential function. Instead, if we consider the source term to be abs(sin(x)) then we get the following synthetic seismogram.

Here, we can still see the peaks are 0.5,0.9 and 1.1 seconds but there are some wiggles are it. This is the effect of the source function. We have considered the same number of modes and other parameters.

When we consider the sinc function as the source function then the seismogram wiggles surrounding the peak decreases.

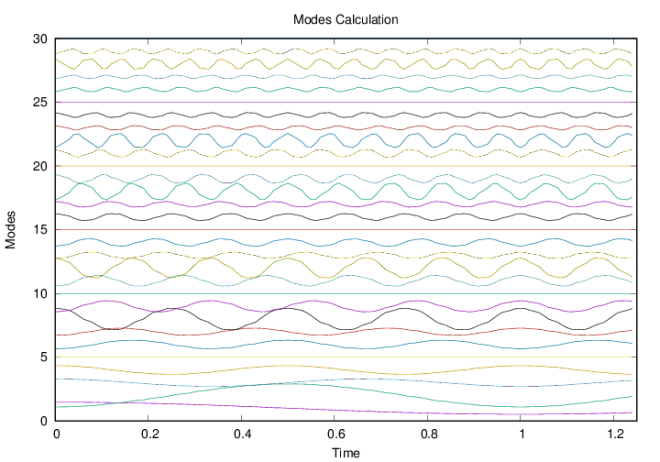
Conclusion:

In this study, we have obtained the synthetic seismogram using the normal mode summation method. We now have two ways to think of the displacement of a traveling wave, propagating waves or normal modes. These two ways can give different interesting insights about the properties of the source and the medium. The difference between the two is that in the propagating wave formulation, the travel times are measured to infer the velocity of the medium and in the normal mode formulation, eigenfrequecies are measured to infer the velocity.

The normal mode solution gives us information about the medium in which the waves propagate and the source that generates them. The physical properties of the string control its velocity (or eigenfunctions and eigenfrequencies). The displacement obtained can be used to study the source that excited them.

In normal mode solution, we sum all the modes to obtain the synthetic seismogram. The individual modes, though, are not physically meaningful. Each mode actually start vibrating even before the wave reaches the end of the string. But when all the modes are summed, the resulting wave propagate at the correct velocity.

In this study, we have considered a uniform string to calculate the synthetic seismogram. We could generalize this idea to obtain the modes of the non-uniform string. We can consider this case in the future posts. We can even calculate the modes for an sphere.

• Utpal Kumar (IES, Academia Sinica)

Constrained Least Square Fitting

Let us try to understand the least square fitting method using an example:

Example

Understanding Seismograms

Seismograms are basic information about earthquakes, chemical and nuclear explosions, mining induced earthquakes, rock bursts and other events generating seismic waves.

Seismograms reflect the combined influence of the seismic source, the propagation paths, the frequency response of the recording instrument and the ambient noise at the recording site.

u(t) = s(t)*g(t)*i(t)*n(t).         “*” means convolution.

where, u is the seismic record, s is the source effect, g is the propagation effect, i is the instrument effect and n is the noise.

So, by understanding seismogram we can understand the seismic source, earth structure, and the noise in the medium.

This is our short attempt to understand the seismograms.

Understanding Seismograms 1

For understanding the seismogram, there are two main things we should notice- record duration and the dispersion. Due to different nature of the propagation velocity of the seismic waves and the different propagation paths taken by them to the station, travel time differences between the main group usually grows with distance. Since the body wave groups do not disperses, so their individual duration remains more or less constant, only the time difference between them changes with distance.

Figure 1: Event-Station Distribution map for the event in Mindanao, Phillipines Island (2005-02-05, Mw-7). The source is 540 km deep.

Figure 2

Figure 3

Figure 4

The epicentral distance for QIZ, BJT and DGAR is ~ 19, 35, 52 degrees respectively. For the station BJT (Figure 3), the epicentral distance is 35.2 degrees and for the station DGAR (Figure 4), the epicentral distance is 52.4 degrees. The P-S arrival times for the station BJT is nearly 300 sec and for the station DGAR, the P-S arrival time is nearly 400 sec. For the station QIZ, it is only around 200 sec. So, with the increase in epicentral distance, the difference in individual phase arrival increases. Also for the station DGAR, the P arrival is later than the BJT.

The time difference between main body wave onsets is:

Distance (degrees) less than	Time-difference in body wave onsets (P-S) in sec
10	180
60 (Fig 1,2,3)	960
100	1800
180	2700

Figure 5 : Travel-Time curve for depth 540 km

For the deep events, we do not see the first arrival as P wave (Figure 6) for short distances (D

Figure 6

Figure 6, is the seismogram at 2 degrees epicentral distance from the deep source. Here, we can notice that the first arrival is not P but the core reflected phase PcP. It is also cevident from the travel time curve(Figure 5).

Figure 7: Event-Station Distribution Map of Near Coast of Peru (2001-06-23, Mw-8.3). The source is at 2 km depth.

When the source is near the surface then we observe the surface waves as well in the seismogram.The surface waves from earthquakes at intermediate (> 70 km) or great depth (> 300 km) may have amplitudes smaller than those of body waves or may not even be detected on seismic records.

In contrast to the body waves, the velocity of surface waves is frequency dependent and hence it is dispersed. The duration of Love and Rayleigh waves increases with distance. As for station NNA (Figure 8), the duration of the first group of Rayleigh wave is about 230 seconds and for station HKT (Figure 9), the duration is around 600 seconds.

We can also notice that for shallower earthquake event, P-wave is the first arrival for stations less than 10 degrees of the source (Figure 10).

Figure 8

In Figure 8, we can notice that for surface waves, the largers periods arrive first than the lowers periods. This is the general case for normal layering. The larger periods sample the higher depths and since the velocity for higher depths is larger so it arrives before the shorter period waves.

Figure 9

In figure 9, for the surface waves, we can observe the wave groups or the beating effect (analogous to acoustics). This is because of the interference of the two or more harmonic waves with closer frequencies or periods.

Figure 10: Travel time curve for depth 2.2km

For certain distance ranges, the travel time curves for different types of seismic phases are close to each other or can even overlap (Figure 5,11).

(a)

(b)

 Figure 11: S, SKS and ScS are very close to each other.

The amplitude of P-wave depends not only on the epicentral distance but on the site effect (underground geology and crustal heterogeneity), azimuth etc.

The most obvious indication on a seismogram that a large earthquake has a deep focus is the small amplitude of the surface waves with respect to the body-wave amplitudes and the P and S waveforms often have impulsive onsets.

A more precise determination of the depth h of a seismic source, however, requires either the availability of a seismic network with at least one station being very near to the source, e.g., at an epicentral distance D < h (because only in the near range the travel time t(D, h) of the direct P wave varies strongly with source depth h), or the identification of seismic depthphases on the seismic record.

At distant seismograph stations, the depth phases pP or sP follow the direct P wave by a time interval that changes only slowly with distance but rapidly with depth.

Inverse Theory

We follow the Geophysical Data Analysis: Discrete Inverse Theory by William Menke book.

We solve the chapters and try to make the things more simpler and faster to read and understand.

Chapter 1: Probability Theory

Click the link below to download the notes:

Probability Theory

Chapter 2: Solution of the Linear, Gaussian Inverse Problem : The length method

Linear, Gaussian Inverse Problem 1

Chapter 3: Solution of the Linear, Gaussian Inverse Problem : Generalized Inverses

Linear, Gaussian Inverse Problem 2

Stay tuned for the other chapters…

Moment Tensor Calculations

Programs:

1. moment_tensor_calc2.pl –> it calculates the moment tensor matrix for given M0, strike, dip and rake

2. diagonalizing_matrix.pl –> this program diagonalizes the given matrix. It can be used to diagonalize the moment tensor matrix as well.

3. iso_dev_mt.pl –> it gives the isotropic and deviatoric part for a given moment tensor matrix

4. maj_min_dc.pl –> this gives the major and minor double couple as output.

5. dc_clvd_mt.pl –> this gives the double couple and clvd part as output.

6. focal_mech_info.pl –> this gives the auxiliary fault plane as output for a given main fault plane.

7. plot_focal_mech.sh –> this bash script plots the focal mechanism solution for a given strike, dip and rake. It makes use of the focal_mech_info.pl program.

Example Focal Mechanism Plot for:

Main Fault

Strike = 40 degrees

Dip = 50 degrees

Rake = 60 degrees

Click here for the plot